栤戣
悢楍{An}偼惍悢p傪弶崁偲偟丄岞嵎3偺摍嵎悢楍丄
悢楍{Bn}偼惍悢3p傪弶崁偲偟丄岞嵎1偺摍嵎悢楍偱偁傞丅
Sn=嚁k=1乣n|Ak-Bk| 傪p偺娭悢偲峫偊偰丄偦偺嵟彫抣傪n傪梡偄偰昞偟側偝偄丅
夝摎
忦審傛傝丄
丂An=3n+p-3
丂Bn=n+3p-1
傛偭偰丄
丂Ak-Bk=2k-2p-2
Ak-Bk=0 偲側傞偺偼丄k=p+1 偺偲偒丅
1) p+1亝1 偺偲偒丄1亝k亝n 偺慡斖埻偵偍偄偰丄k亞p+1 側偺偱
丂|Ak-Bk|=Ak-Bk
傛偭偰丄
丂Sn=嚁k=1乣n(Ak-Bk)=嚁k=1乣n(2k-2p-2)
丂丂=嚁k=1乣n2k-嚁k=1乣n(2p+2)
丂丂=n(n+1)-n(2p+2)
丂丂=-2np+n2-n
2) 1亙p+1亙n 偺偲偒
丂1亝k亝p 偺偲偒丂|Ak-Bk|=Bk-Ak
丂p+1亝k亝n 偺偲偒丂|Ak-Bk|=Ak-Bk
傛偭偰丄
丂Sn=嚁k=1乣p(Bk-Ak)+嚁k=p+1乣n(Ak-Bk)
丂丂=嚁k=1乣p(-2k+2p+2)+嚁k=p+1乣n(2k-2p-2)
丂丂=-p(p+1)+p(2p+2)+{0+2+4+丒丒丒+(2n-2p-2)}
丂丂=p(p+1) + 2{0+1+2+丒丒丒+(n-p-1)}
丂丂=p(p+1) + (n-p-1)(n-p)
丂丂=2p2+2(1-n)p+n2-n
丂丂2{p+(1-n)/2}2 + (n2-1)/2
3)n亝p+1 偺偲偒丄1亝k亝n 偺慡斖埻偵偍偄偰丄k亝p+1 側偺偱
丂|Ak-Bk|=Bk-Ak
傛偭偰丄
丂Sn=嚁k=1乣n(Bk-Ak)=嚁k=1乣n(-2k+2p+2)
丂丂=-嚁k=1乣n2k+嚁k=1乣n(2p+2)
丂丂=-n(n+1)+n(2p+2)
丂丂=2np-n2+n
埲忋傛傝丄Sn 偲 p 偺娭學傪僌儔僼偵偡傞偲丄埲壓偺傛偆偵側傞丅
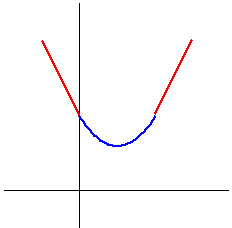
愒偑捈慄丄惵偑曻暔慄偱偡丅
Sn 偺嵟彫抣偼曻暔慄偺捀揰晅嬤偵偁傞偙偲偑傢偐傝傑偡丅
捀揰偼((n-1)/2, (n2-1)/2) 偱偡丅
(n-1)/2 偑惍悢偺帪偼丄捀揰偑嵟彫偺揰偲側傝傑偡丅
(n-1)/2偑惍悢偱側偄偲偒偼丄捀揰偵堦斣嬤偄奿巕揰偑嵟彫偺揰偵側傝傑偡丅
n偑婏悢偺帪 p=(n-1)/2 偺偲偒 Sn 偼嵟彫抣 (n2-1)/2丅
n偑嬼悢偺帪偼丄p=(n-1)/2+1/2 傑偨偼 p=(n-1)/2-1/2 偮傑傝丄
丂p=n/2 傑偨偼 p=n/2-1 偺偲偒 Sn 偼嵟彫抣 n2/2
乮Sn = 2{p+(1-n)/2}2 + (n2-1)/2 偵 p=n/2 傪戙擖偟偰媮傔傑偡丅
丂p=n/2-1 傪戙擖偟偰傕摨條乯
乽嶼悢丒悢妛乿偺晹壆偵栠傞