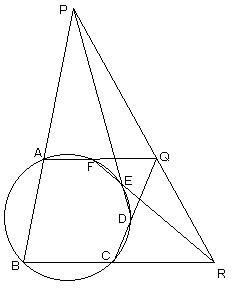
パスカルの定理
　円に内接する六角形の相対する３組の辺の延長の交点は１直線上にある。

証明

３点Ｑ，Ｆ，Ｃを通る円を描き、 この円とＢＲ、ＦＲとの交点をＫ，Ｌとする。	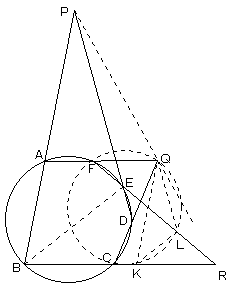	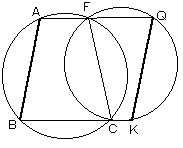四角形ＡＢＣＦと四角形ＦＣＫＱはともに円に内接するので、 　∠ＡＢＣ＝∠ＱＦＣ＝∠ＱＫＲ よって、ＡＢ//ＱＫ　………(1)
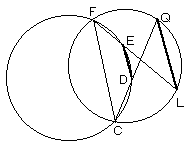		円に内接する四角形ＥＦＣＤにおいて、 　∠ＦＣＤ＝∠ＤＥＬ また、円周角により 　∠ＦＣＤ＝∠ＥＬＱ よって、∠ＤＥＬ＝∠ＥＬＱ　より 　ＥＤ//ＱＬ
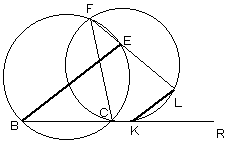		円周角により、 　∠ＥＢＣ＝∠ＥＦＣ 円に内接する四角形ＦＣＫＬにおいて、 　∠ＥＦＣ＝∠ＬＫＲ よって、∠ＥＢＣ＝∠ＬＫＲより、 　ＢＥ//ＫＬ

以上より、△ＰＢＥと△ＱＫＬは、対応する辺がすべて平行となり、ＰＱ，ＥＬ，ＢＫは１点Ｒで交わる。

「算数・数学の部屋」に戻る