ブラマーググプタの定理
　円に内接する四角形 ABCD の対角線が直交しているとき、
　AB の中点 M と対角線の交点 E を結ぶ直線は、CD に垂直である。
　また、対角線の交点 E から CD へ下ろした垂線CH の延長線は、辺 AB の中点 M を通る。

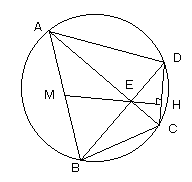
証明
（１）Ｍが中点ならば、ＭＥはＣＤに垂直　の証明
　∠ＡＥＢ＝９０°より、
　　ＡＭ＝ＢＭ＝ＥＭ
　よって、△ＭＥＢは二等辺三角形となり、
　　∠ＭＢＥ＝∠ＭＥＢ
　さらに、対頂角と、円周角より、
　　∠ＭＢＥ＝∠ＭＥＢ＝∠ＤＥＨ＝∠ＤＣＥ　・・・(i)
　∠ＤＥＣ＝９０°より、△ＤＥＣの残りの角について、
　　∠ＥＤＣ＋∠ＥＣＤ＝９０°
　(i) より、
　∠ＥＤＣ＋∠ＤＥＨ＝９０°
　よって、△ＥＤＨにおいて、∠ＥＨＤ＝９０°
（２）ＥＨがＣＤに垂直ならば、その延長線とＡＢの交点ＭはＡＢの中点である　の証明
　条件より、
　　∠ＤＥＨ＝∠ＤＣＥ
　さらに、対頂角と、円周角より、
　　∠ＤＥＨ＝∠ＤＣＥ＝∠ＭＥＢ＝∠ＭＢＥ　・・・(ii)　※(i) と同型
　よって、ＭＥ＝ＭＢ　となり、
　　∠ＡＥＭ＝９０°−∠ＭＥＢ＝９０°−∠ＭＢＥ
　一方、∠ＭＢＥ＋∠ＭＡＥ＝９０°　より、
　　∠ＭＡＥ＝∠ＭＥＡ
　よって、ＡＭ＝ＭＥ　となり、ＭＡ＝ＭＢ　が導け、
　ＥＨとＡＢの交点ＭはＡＢの中点である。

「算数・数学の部屋」に戻る