5問あります。
質問1:点Pから2円x2+y2=4、(x−4)2+(y−5)2=9に引いた
接線の長さが等しい点Pの軌跡を求めよ。
解答1:
円の接線の長さの公式より、
点P(x、y)について、
x2+y2−4=(x−4)2+(y−5)2−9
が成り立つ。
整理して、
8x+10y=36
y=−0.8x+3.6・・・(1)
逆に、直線 (1) 上の任意の点を (m, -0.8m+3.6) とすると、
x2+y2=4
までの接線の長さは
m^2+(−0.8m+3.6)^2−4
=1.64m^2−5.76m+8.96
一方、
(x−4)2+(y−5)2=9
までの接線の長さは
(m−4)2+(−0.8m−1.4)2−9
=1.64m^2−5.76m+8.96
となり、両者は等しくなる。
答え:直線 8x+10y=36
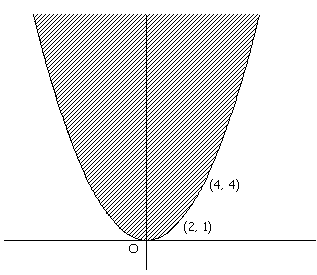
質問2:放物線y=x2+ax+bとx軸との共有点が存在しないとき、点(a,b)の存在する範囲を図示せよ。
解答2:
判別式Dを計算して、
D=a^2−4b<0
点(a,b)は、
y>x^2/4
の範囲に存在する。
質問3:円x2+y2=1と直線ax+by+2=0が異なる2点で交わるとき、点(a,b)の存在する範囲を図示せよ。
解答3:
点と直線の距離の公式より、
原点から、直線ax+by+2=0 までの距離は、
2/√(a^2+b^2)
であり、これが円の半径1未満であれば、条件を満たす。
2/√(a^2+b^2)<1
aとbがともに0になることはないので、
√(a^2+b^2)>0
これを両辺に掛けて、
2<√(a^2+b^2)
両辺ともに正なので、2乗して、
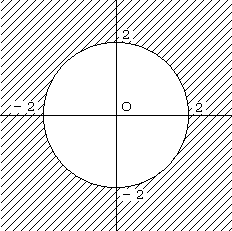
4<a^2+b^2
よって、点(a,b)の存在する範囲は、以下のようになる。
質問4:
2次方程式x2-2px+(p+2)=0の2つの解がともに1より大きくなるようなpの値の範囲を求めよ。
解答4:
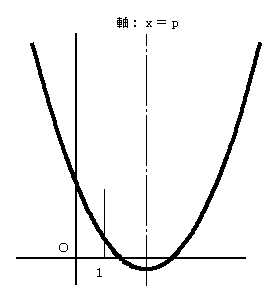
y=x2−2px+(p+2)=0
のグラフが、図のような位置にあればよい。
そのためには、
・軸がx=1よりも右にある。
・x=1のとき y>0
・判別式>0
であればよい。
これらを式にすると、
p>1・・・(1)
1−2p+(p+2)>0・・・(2)
p^2−(p+2)>0・・・(3)
となる。
(2) より、
p<3・・・(2)'
(3) より、
(p+1)(p−2)>0
p<−1 または p>2・・・(3)'
(1),(2)',(3)' より、
2<p<3・・・答え
質問5:整式p(x)をx-1で割ると3余り、x-2で割ると10余る。p(x)を x2−3x+2
で割ったときの余りを求めよ。
解答5:
剰余定理より、
p(1)=3
p(2)=10
また、p(x)を x2−3x+2=(x−1)(x−2) で割ったときの、商をq(x)、余りを
ax+bとおくと、
p(x)=(x−1)(x−2)q(x)+ax+b
と書ける。x=1,x=2を代入すると、
p(1)=a+b=3・・・(1)
p(2)=2a+b=10・・・(2)
この連立方程式を解いて、
a=7、b=−4
答え:7x−4
円の接線の長さの公式
円 (x−a)2+(y−b)2=r2 に、円外の点P(m、n)から接線を引いたときの
接点をQとするとき、接線の長さPQを考える。
円の中心は 点A(a、b)であり、△PQAは∠PQA=90°の直角三角形である。
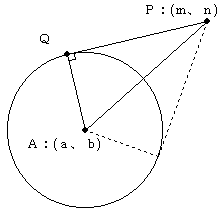
PA2=(m−a)2+(n−b)2
QA2=r2
より、
PQ2=PA2−QA2=(m−a)2+(n−b)2−r2
PQ=√{(m−a)2+(n−b)2−r2}
点と直線の距離の公式
点(x0, y0) から、直線 ax+by+c=0 までの距離は
|ax0+by0+c|/√(a^2+b^2)
特に、原点からの距離は、
|c|/√(a^2+b^2)