問題:
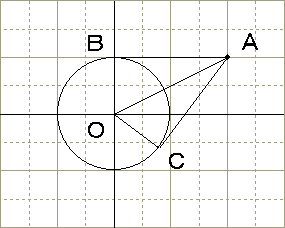
点A(2,1)から円 x2+y2=1 に引いた接線の方程式と接点の座標を求めよ。
解答1:
点A(2,1)を通る直線を
y=a(x−2)+1 ・・・・(1)
とおく。
※(1) の式では、y軸に平行な直線(x=1 など)は表せないが、そういう接線はあり得ないことは図から明らかなので、(1) の式で十分である。
厳密には a(x−2)+b(y−1)=0 とする。
x2+y2=1 ・・・・(2)
(1) を (2) に代入して、
x2+{a(x−2)+1}2=1
x2+a2(x2−4x+4)+2a(x−2)+1=1
(a2+1)x2+2(a−2a2)x+(4a2−4a)=0 ・・・(3)
これが重解を持つためには、判別式をとって、
D/4=(a−2a2)2−(a2+1)(4a2−4a)
=4a4−4a3+a2−(4a4−4a3+4a2−4a)
=−3a2+4a
=a(−3a+4)=0
これより、a=0,4/3
1. a=0 のとき
(1) より 接線の方程式は、
y=1
(3) より
x2=0
x=0(重解)
よって、接点の座標は(0,1)
2. a=4/3 のとき
(1) より 接線の方程式は、
y=4/3(x−2)+1 ・・・・(4)
3y=4(x−2)+3
3y=4x−5
4x−3y−5=0
(3) より
25/9x2−40/9+16/9=0
25x2−40x+16=0
(5x−4)2=0
x=4/5(重解)
(4) に代入して
y=−3/5
よって、接点の座標は(4/5,−3/5)
答え:接線の方程式 y=1 のとき 接点の座標(0,1)
接線の方程式 4x−3y−5=0 のとき 接点の座標(4/5,−3/5)
解答2:
接点の座標を(x0,y0)とする。
この接点における接線の方程式は、
x0x+y0y=1
と書ける。
これが点A(2,1)を通るから、
2x0+y0=1
y0=−2x0+1 ・・・・(1)
また、点(x0,y0)は円
x2+y2=1
上の点なので、
x02+y02=1 ・・・・(2)
(1) を (2) に代入して、
x02+(−2x0+1)2=1
x02+4x02−4x0+1=1
x0(5x0−4)=0
x0=0,4/5
1.x0=0 のとき
(1) より、
y0=1
点(0,1)が接点の座標であり、この点と点A(2,1)を結ぶ直線の式は、
y=1
2. x0=4/5 のとき
(1) より
y0=−3/5
点(4/5,−3/5)が接点の座標であり、この点と点A(2,1)を結ぶ直線の式は、傾きが
(1+3/5)/(2−4/5)=8/6=4/3
であるので、接線の式は
3(y−1)=4(x−2)
3y−3=4x−8
4x−3y−5
答え:接線の方程式 y=1 のとき 接点の座標(0,1)
接線の方程式 4x−3y−5=0 のとき 接点の座標(4/5,−3/5)
解答3−1:
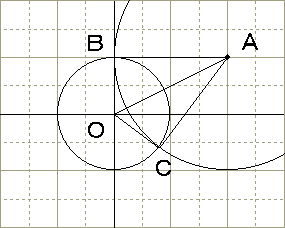
図より、接点の一つが点B(0,1)であることは明らか。
そこで、点Aを中心にして半径2(=ABの距離)の円
(x−2)2+(y−1)2=4 ・・・・(1)
を描き、円
x2+y2=1 ・・・・(2)
との、もう一方の交点がもうひとつの接点となる。
(1) を変形して、
x2+y2−4x−2y+1=0
(2) を代入して、
1−4x−2y+1=0
2x+y−1=0
これを、(2) に代入して (以下略)
解答3−2:
直線BCは直線OAと直交するので、その傾きは−2である。(OAの傾きは-1/2 であるため)
直線BCの式は、
y=−2x+1
これを、(2) に代入して (以下略)
解答4:
∠OBA=90°、∠OCA=90°
より、2つの接点B、Cは、OAを直径とする円上にある。
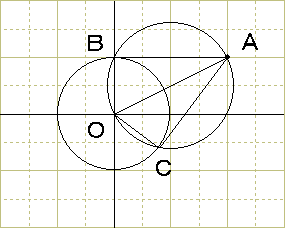
OAの中心は(1,1/2)、OA=√5 なので、半径は√(5/4)
円の式は
(x−1)2+(y−1/2)2=5/4 ・・・・(1)
整理して、
x2+y2−2x−y=0
x2+y2=1 ・・・・(2)
を代入して、
1−2x−y=0
y=−2x+1
これを、(2) に代入して (以下略)
「算数・数学の部屋」に戻る