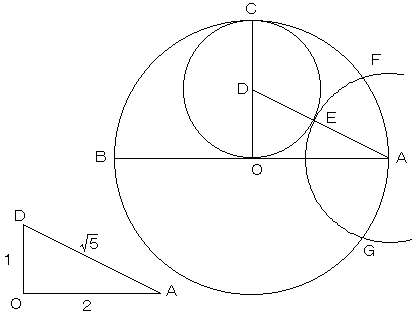
正五角形の作図

実際には、正十角形の作図をして、点を2つおきに結んで正五角形にします。
図の∠FOAが36°になれば正十角形の作図の完成です。
円の半径を2とすると、公式※により、FAの長さは√5−1になります。
√5を作るために、左下図のような、1:2:√5の直角三角形を利用します。
これらを、効率よく作るように図をまとめると、上図のようになります。
(手順)
点Oを中心とした円(円1)と、円1に内接する半径が半分の円(円2)を描きます。
円1と円2の接点を点C、円2の中心を点Dとし、点Oにおける円2の接線(円1の直径になります)
を引き、円1との交点を点A、点Bとします。
線分ADと円2の交点を点Eとし、点Aを中心とし点Eを通る円(円3)を描きます。
円1と円3との交点を点F、点Gとするとき、線分FGの長さで円1を切れば、正五角形、
線分AFの長さで円1を切れば、正十角形が描けます。
※AFの長さは、以下のようにしても求められます。
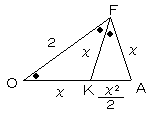
上図において、
OF=OA=2
∠FOA=∠OFK=∠AFK=36°
です。また、AF=x とおくと、
OK=FK=AF=x
△OAF と △FAK は相似ですから、
2:x=x:AK
より、
AK=x2/2
よって、OAにおいて、
x2/2+x=2
x2+2x−4=0
これを解いて、
x=−1±√(1+4)
x>0より、
x=AF=√5−1
「算数・数学の部屋」に戻る