ｄｏｏさんからの質問１

ｄｏｏさんからの質問１

問題　f(x)=x²+2ax+b　　(0≦x≦5)
　　　が最大値６，最小値－３をもつように，定数a,bの値を求めよ。

解答
　　f(x)=x²+2ax+b
　　　　=(x+a)²-a²+b
　　より、y=f(x) のグラフは以下の４通りが考えられ、それぞれａ，ｂの値が決まります。

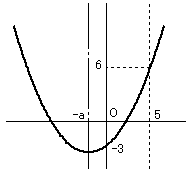
a≧0のとき
f(0)=-3 かつ f(5)=6
f(0)=b=-3 より b=-3
f(5)=10a+b+25
　　=10a+22=6
より a=-1.6
となり a≧0 に不適

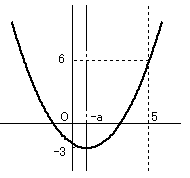
-2.5≦a＜0 のとき
f(-a)=-3 かつ f(5)=6
f(-a)=-a²+b=-3
f(5)=10a+b+25=6
これを解いて
(a,b)=(-2,1),(-8,61)
-2.5≦a≦0 より
(a,b)=(-2,1)

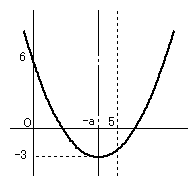
-5≦a＜-2.5 のとき
f(0)=6 かつ f(-a)=-3
f(0)=b=6 より b=6
f(-a)=-a²+b=-a²+6=-3
より a²=9　，a=±3
-5≦a＜-2.5 より
(a,b)=(-3,6)

a＜-5 のとき
f(0)=6 かつ f(5)=-3
f(0)=b=6 より b=6
f(5)=10a+b+25
　　=10a+31=-3
より a=-3.4
となり a＜-5 に不適

以上より、
答え　ａ＝－２，ｂ＝１　または　ａ＝－３，ｂ＝６

急いで解いたから、間違ってるかも(^^;