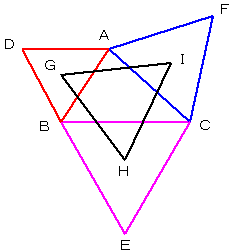
ナポレオンの三角形

図のように△ＡＢＣの３辺の外側に正三角形ＡＢＤ、ＢＣＥ、ＡＣＦを作り、それぞれの正三角形の重心をＧ，Ｈ，Ｉとするとき、△ＧＨＩは正三角形となる。

ナポレオンの三角形（外側）

＜証明＞

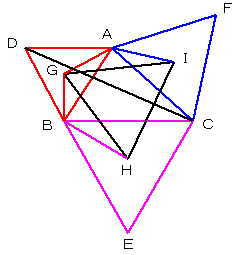
△ＡＤＣと△ＡＧＩにおいて、
　∠ＤＡＣ＝∠ＢＡＣ＋∠ＤＡＢ＝∠ＢＡＣ＋６０°
　∠ＧＡＩ＝∠ＢＡＣ＋∠ＧＡＢ＋∠ＣＡＩ＝∠ＢＡＣ＋３０°＋３０°＝∠ＢＡＣ＋６０°
より、
　∠ＤＡＣ＝∠ＧＡＩ　・・・(1)
また、
　ＡＧ＝ＡＤ／√３　　・・・(2)
　ＡＩ＝ＡＣ／√３　　・・・(3)
(1)(2)(3) より、２辺の比とその挟む角が等しいので、
　△ＡＤＣと△ＡＧＩは相似。
また、
　∠ＤＡＧ＝３０°
より、ＧＩはＤＣを時計回りに３０°回転した位置にある。

△ＢＤＣと△ＢＧＨにおいて、
　∠ＤＢＣ＝∠ＡＢＣ＋∠ＤＢＡ＝∠ＡＢＣ＋６０°
　∠ＧＢＨ＝∠ＡＢＣ＋∠ＧＢＡ＋∠ＣＢＨ＝∠ＡＢＣ＋３０°＋３０°＝∠ＡＢＣ＋６０°
より、
　∠ＤＢＣ＝∠ＧＢＨ　・・・(4)
また、
　ＢＧ＝ＢＤ／√３　　・・・(5)
　ＢＨ＝ＢＣ／√３　　・・・(6)
(4)(5)(6) より、２辺の比とその挟む角が等しいので、
　△ＢＤＣと△ＢＧＨは相似。
また、
　∠ＤＢＧ＝３０°
より、ＧＨはＤＣを反時計回りに３０°回転した位置にある。

以上より、
　ＧＩ＝ＧＨ
　∠ＩＧＨ＝６０°
より、△ＧＨＩは正三角形である。

　　　　　　　　　　　　　　　　　　　　　　　証明終

「算数・数学の部屋」に戻る