ナポレオンの三角形

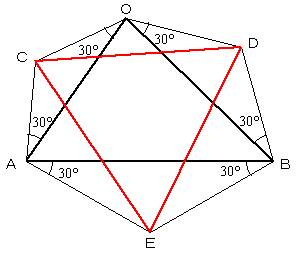
図のように△ＯＡＢの３辺の外側に両底角が３０°の二等辺三角形を立てたとき△ＣＤＥは正三角形となる。
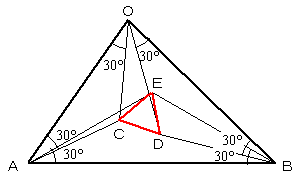
また、△ＯＡＢの３辺の内側に同様の二等辺三角形を作ったときも、△ＣＤＥは正三角形となる。

ナポレオンの三角形（外側）	ナポレオンの三角形（内側）

＜証明＞
△ＯＡＢを９０°回転させ、かつ倍に縮小します。

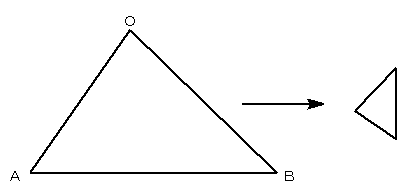
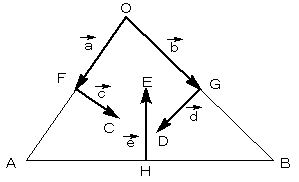
その各辺を、△ＯＡＢの互いに垂直な辺の中点Ｆ、Ｇ、Ｈに立てます。

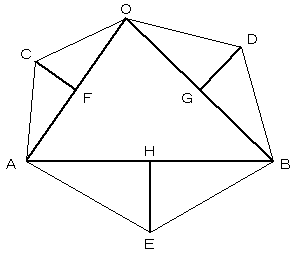
このとき、図の点Ｃ，Ｄ，Ｅ がナポレオンの三角形（外側）になっています。

ここで、図のようにベクトルを決めます。

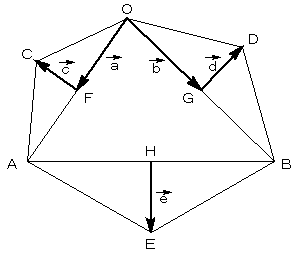
このとき、以下の性質が成り立ちます。
　　
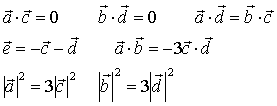
なお、この性質は、ナポレオンの三角形（内側）についても成り立つので、以下の証明で、
外側、内側両方の証明をしたことになります。

はそれぞれ、
　　
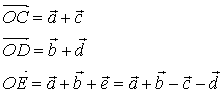
となり、これを用いて、 およびその長さを求めると以下のようになります。
　　
　　
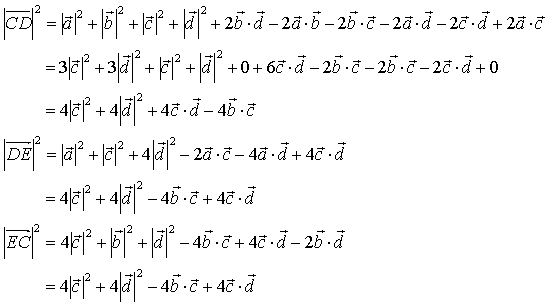
以上より、
　　
となり、△ＣＤＥは正三角形となります。　　　　　　　　　証明終

「算数・数学の部屋」に戻る