問題
a,bを0<a<bを満たす定数とする。
初項A1=a,第二項A2=b である等差数列{An} (n=1,2,3・・) に対して、
xy平面の直線Lnを
Ln : Anx-An+1y+An+2=0 (n=1,2,3・・)
とする。
(1) Lnはnの値にかかわらずある定点を通ることを示せ。
(2)p>2をみたすpに対して領域DをD={(x、y)│x≧p、y≦p}とするとき、
どのようなnに対しても、LnとDが共有点をもたないためのpについての条件を求めよ。
解答
(1)
初項A1=a,第二項A2=b なので、この数列の公差は b−a です。
すると、初項a、公差b−aの等差数列の一般項は
An=a+(b−a)(n−1)=(b−a)n+2a−b
と書けます。これを、Anx-An+1y+An+2=0 に代入すると、
{(b-a)n+2a-b}x - {(b-a)n+a}y + {(b-a)n+b} = 0
n{(b-a)x - (b-a)y + (b-a)} + {(2a-b)x - ay +b} = 0
これが、n についての恒等式となるためには、
(b-a)x - (b-a)y + (b-a) = 0 ・・・(i) かつ
(2a-b)x - ay +b = 0 ・・・(ii)
b-a>0 より、(i) の両辺を(b-a) で割って、
x - y + 1 = 0 ・・・(i)'
と書けます。これと(ii)の連立方程式を解いて、
x=1,y=2
よって、Ln は常に点(1,2)を通ります。
(2)
Ln の傾きを dn とすると、dn=An/An+1 ですが、これは、
d1=a/b より、 0<d1<1
n→∞ のとき、dn→1 になります。
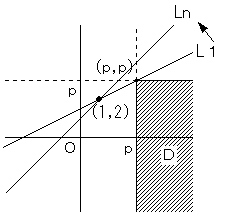
一方、D は、図のような領域なので、L1 が、Dに触れなければ、他のLnは、
点(p,p)から離れる方向なので、L1 が、点(p,p) に触れるときが、p の限界となります。
L1:ax - by + 2b-a = 0
と、直線 y=x との交点は x=y=(2b-a)/(b-a) より、
2<p<(2b-a)/(b-a)
が、pの条件となります。
「算数・数学」の部屋に戻る