あゆみさんからの質問1
分数の割り算って割る数を分母と分子を逆にしますよね。どうして,逆にするのですか。
解答
この解説はかなり長い。要点だけ知りたい人はこっち。
まず、この方法でまちがいないということをかくにんしよう。
<例題1> 10リットルの水を2リットルのバケツでくみ出すと何回でくむことができるか?
これは、明らかに 10÷2=5 で 5回だ。では、
<例題2> 4/5(5分の4)リットルの水を 2/15(15分の2)リットルのコップで
くみ出すと何回でくむことができるか?
例題1に比べて 10→4/5、2→2/15 になっただけなので、計算する式は
4/5÷2/15 だ。
試しに2/15をいくつも足していくと
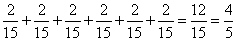
のように、6回足すと4/5になるので、6回で水をくむことができる、つまり、この問題の答えは
6回だ。
当然、4/5÷2/15 の答えも6になるはずだ。
これを「分母と分子を逆にしてかける」方法を使うと、
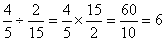
となり、どうやら、この方法はまちがってはいないようだ。
では、なぜそれでいいのだろう?
学校では、分数を習う前に、1,2,3という整数を使っていろんな計算を勉強してきたはずだ。
そして、そんな数の計算には、いくつかの性質があった。たとえば、
(性質1)3×4=12と4×3=12のように、かけ算は順序を変えても答えは変わらない。
(性質2)4×3×2=24、4×(3×2)=24 のように、3と2を2度に分けてかけても、3と2を
先に掛けておき、あとでまとめてかけても答えは変わらない。
(性質3)24÷3÷2=4、24÷(3×2)=4 のように、3と2で2度に分けて割っても、3と2を
先に掛けておき、あとでまとめて割っても答えは変わらない。
などだ。実際に計算して、確かめてみよう。
このような、整数の計算での性質は、数字が分数になっても、小数になっても同じように使っていいはずだ。
また、次の計算を考えよう。
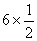
かけ算は順序を変えても答えは変わらないので、1/2を6倍すると考えよう。
6倍するとは、6回足すことだから、1/2を6回足して、答えは3だ。
こういう問題をもっといっぱい調べると
「1/2をかけるということは、2で割るのと同じことである」
ということがわかる。確かに、6が3になってしまったから、2で割ったのと同じだ。
かける数を変えて、もっといっぱい調べると
「1/3をかけるということは3で割るのと同じ」
「1/4をかけるということは4で割るのと同じ」
など、すべての整数について、同じことがいえる。つまり、
(性質4)1/nをかけることは、nで割るのと同じである
ここで、nには、0でないいろんな数が当てはまるよ。
さて、今度はわり算だ。
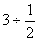
これを、さっきと同じように「3リットルの水を1/2リットルのコップでくみ出すには何回でくめるか」
と考えると、6回でくみ出せる。
こういう問題をもっといっぱい調べると
「1/2でわるということは、2をかけるのと同じことである」
ということがわかる。確かに、3が6になったのだから、2をかけたのと同じだ。
割る数を変えて、もっといっぱい調べると
「1/3で割るということは3をかけるのと同じ」
「1/4で割るということは4をかけるのと同じ」
など、すべての整数について、同じことがいえる。つまり、
(性質5)1/nで割ることは、nをかけるのと同じである
ここまで理解できたかな?
次に進むまでに、必ず理解しよう。
要点はここから
さあ、ここからが要点だが、その前に一言。
「分数で割るときは、分子と分母を逆にしてかける」方法は、あくまで方法であって、これを使っていろんな
分数の計算ができるようになったからといって、やみくもにやり方だけをおぼえたのではいけない。必ず、
計算するときに、数がどのように変化していっているか注意しながら、計算するようにしよう。算数は、計
算のやり方を勉強することではなく、数という規則正しく変化する道具を使って、ものの性質を調べたり、
予測したりすることだからだ。
<例題>
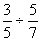
これを次々に変形していくぞ。
5/7は1/7が5つ集まったものだから、5×1/7と書ける。
3/5÷(5×1/7)
性質3を逆に使って、5と1/7とでまとめて割っているのを、別々に割ってもいいだろう。
3/5÷5÷1/7
5で割ることは1/5をかけるのと同じだ(性質4)。
1/7で割るのは7をかけるのと同じだ(性質5)
3/5×1/5×7
1/5と7を別々にかけているのを、まとめてかけてもいいだろう(性質2)
3/5×(1/5×7)
1/5×7 は 7/5 である。
3/5×7/5
どうだろう。5/7で割っていたものが、最後は7/5をかける式になった。
「分数で割るときは、分子と分母を逆にしてかける」方法は、まずもって、おぼえて使えるようにならなければ
いけない。しかし、その裏にはこんなにたくさんの知識が基になっている。やり方をおぼえるのにとどまらず、そ
のしくみを味わってほしい。
算数・数学の部屋に戻る