問題６の答え

問題６の解答

解答を寄せていただいた皆様。ありがとうございました。
中村明海さん、相原朋樹さん、清川育男さん、数楽者さんから解答を寄せていただきました。

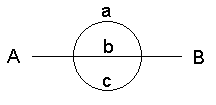
(1)		ａ,ｂ,ｃ３本の道を通る順序は、 (ａ，ｂ，ｃ)　(ａ，ｃ，ｂ) (ｂ，ａ，ｃ)　(ｂ，ｃ，ａ) (ｃ，ａ，ｂ)　(ｃ，ｂ，ａ) の６通り。式で書くと、３×２×１＝６答え：６通り
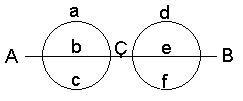
(2)		ＡからＣまで行くのに６通り、ＣからＢまで行くのに６通りですから、６×６＝３６答え：３６通り
(3)	(2) の３６通りの組み合わせの１つ、例えば(a,b,c)－(d,e,f) について、ａを通って、円と円の接点（節『ふし』と呼ぶことにします）まで来たあと、・左の円を先に描く手順　(a,b,c,d,e,f) ・右の円を先に描く手順　(a,d,e,b,c,f) の２通りに分かれます。よって、３６×２＝７２　　　　答え：７２通り
(4)	(3) と同じように考えると、節に来るごとに、左に戻る、右に進むの２通りの分岐があります。１つ１つの円の描き方：６ⁿ通り・・・円がｎ個節での分岐の選び方　：２^n-1通り・・・節がｎ－１個以上より　答え　６ⁿ×２^n-1 通り